Über die Thematik der Stabilitätsberechnung für Segelschiffsmodelle ist schon so viel geschrieben worden, dass es auf einen Beitrag mehr oder weniger nicht ankommt. Sicher weiß ich auch nichts Neues zu berichten, ich möchte hier auch nur erzählen, wie ich es bisher gemacht habe. Hierbei hoffe ich, dass es so verständlich ist, dass auch ein Anfänger von meiner Schilderung profitieren kann.
Als Erstes stelle ich den Lateralschwerpunkt fest. Hierzu belade ich die Rumpfschale incl. fertigem Ballastkiel ohne Ruder (mit oder ohne Ruder ist hierbei noch in Frage gestellt; mit Ruder wandert der Lateralschwerpunkt jedenfalls weiter nach achtern), bis der Rumpf bis zur KWL (Konstruktionswasserlinie) eintaucht. Dann schiebe ich ihn mit einem Finger seitlich quer durch das Wasser. Hierbei sollte es sich natürlich um ein größeres Gewässer handeln als die Badewanne. Der Punkt, an dem sich der Rumpf einwandfrei quer durch das Wasser schieben lässt, ohne dass er sich um Bug oder Heck dreht, ist für mich der Lateralschwerpunkt. Zweifler können den Versuch auch beidseitig wiederholen oder - was noch besser wäre - dies mit einem um ca. 30° gekrängten Rumpf (erreicht durch zusätzlichen Trimmballast) vornehmen. Denn hierbei könnte sich eine Verlagerung des Lateralschwerpunktes ergeben, eine Vermittlung beider Punkte wäre dann wahrscheinlich ideal (?). 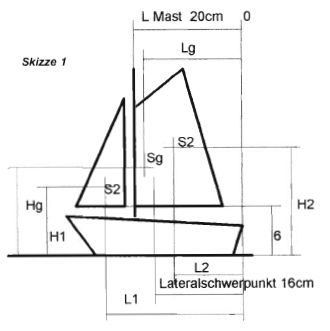
Als Nächstes ist der Segelschwerpunkt festzulegen. Hierbei wende ich immer die rechnerische Methode an. Dies halte ich für wesentlich einfacher als die Anfertigung einer Pappschablone, denn es kommen hierbei doch nur die Grundlagen der Geometrie zur Anwendung. Als Grundformei gilt:
Lg = Summe A x L / A
Lg = Abstand von dem Messpunkt 0
A = Fläche des betreffenden Segels
L = Schwerpunktabstand der Segelfläche zum Messpunkt.
Es können beliebig viele Flächen sein, ferner spielt die Form der Flächen keine Rolle, da jeweils die Fläche und der Abstand des Einzelflächenschwerpunktes zum Einsatz kommt. Zum besseren Verständnis soll Skizze 1 dienen.
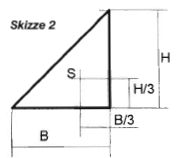
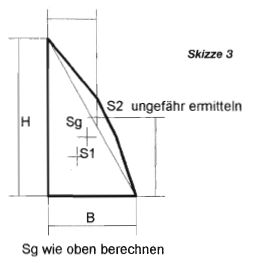
Die Schwerpunkte der einzelnen Flächen errechnen sich gemäß den Skizzen 2 und 3.
Der Schwerpunkt des Dreiecks liegt im Schnittpunkt der Seitenhalbierenden. Die Maße werden aus der Zeichnung herausgemessen.
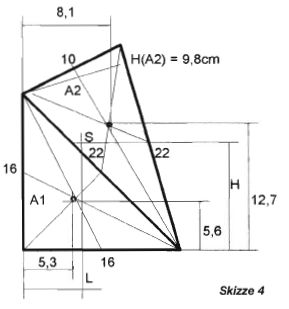
Beim Gaffelsegel wird's etwas schwieriger. Hierbei habe ich die Fläche in zwei Dreiecke zerlegt (siehe Skizze 4).
L=Summe A x L / A
L=A1 x L1 + A2x L2 / A1 + A2
L=128 x 5,3 + 108 x 8,1 / 12 + 108 = 6,6cm
H=A1 x H1 + A2 x H2 / A1 + A2
H=128 x 5,6 + 108 x 12,7 /12 + 108 = 8,8cm
A(2) = 128 + 108 = 236 cm²
A(1) = 21 x 12 / 2 = 126cm²
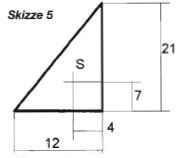 Berechnung nach Skizze 1:
Berechnung nach Skizze 1:
Lg=Summe A x L / A
= A1 x L1 + A2 x L2 / A1 + A2
= 126 x 26 + 236 x 13,4 / 126 + 236 = 17,7cm
Da der Lateralschwerpunkt mit einem Abstand von 16cm angenommen wird, liegt die Mastposition an der richtigen Stelle, denn der Segelschwerpunkt sollte etwas vor dem Lateralschwerpunkt liegen, auch wenn in anderen Veröffentlichungen gegenteilige Ansichten vertreten werden.
Da die vollen Flächen nur bei halbem Wind zur Wirkung kommen, sollten wir auch diesen Fall annehmen. Da bei halbem Wind aber auch die Segel einen Öffnungswinkel von Ca. 30° haben, verschiebt sich der Schwerpunkt um den Cosinuswert des Öffnungswinkels auch noch leicht nach vorn. Ideal wäre es, wenn das Boot bei stetigem Wind geradeaus läuft und in einer Böe, bei Krängung bis zum Decksrand, anluvt.
Die Höhen der einzelnen Flächen habe ich schon festgelegt. Jetzt brauche ich nur noch den Abstand bis zur Wasserlinie (6 cm) hinzuzurechnen.
Die Wasserlinie nehme ich der Einfachheit halber als Drehpunkt an. Und dann kann's losgehen. Als Formel nehme ich an:
Fw x Hg = Vg x Lv
Fw = Windkraft, bei 4 Windstärken (ca. 40 N/m²) ergeben sich bei unserer Segelfläche von 362 cm² Ca. 1,5N.
Da die Segel aber einen Öffnungswinkel von ca 30° haben, verkleinert sich die Fläche um den Cosinuswert des Winkels. Und da ich eine Krängung von ca 30° für maximal halte, verkleinert sich die Fläche nochmals um denselben Wert, folglich auch entsprechend die wirksame Kraft.
F = Fw x (cos a)²
F = 1,5 x 0,86 x 0,86
= ca. 1,125 N.
Hg = Schwerpunktabstand der Segelfläche zur Wasserlinie.
Hg = A1 x H1 + A2 x H2 / A1 + A2
= 126 x 13 + 236 x 14,8 / 12 + 236 = ca 14,2 cm
Vg = Gesamtverdrängung
Lv = Gesarntverdrängungsabstand
Das kann ich nicht, das wäre mir auch viel zu aufwändig. Hat man die Konstruktion rechnergestützt erstellt und verfügt über das entsprechende Programm (evtl. kann es „pro ingenieur"), spuckt der Rechner die Daten aus.
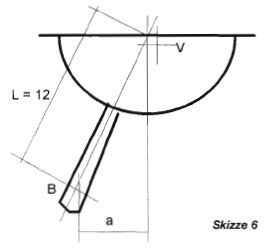
Also behelfe ich mich mit dem Ballastschwerpunkt und dessen Abstand zur Wasserlinie bei einer angenommenen Krängung von 30° (siehe Skizze 6).
Leider kommt nicht der gesamte Abstand zur Wirkung, sondern nur der Abstand zur Senkrechten. Dieser errechnet sich aus der Länge mal dem Sinuswert des Winkels:
a = L x sin 30°
= 12 x 0,5 = 6 cm
Ein zusätzlich aufrichtendes Moment entsteht durch die Neigung und die damit verbundene Vergrößerung der Verdrängung (V). Aber ich denke, diese Kraft und der wirksame Hebelarm wird für uns noch lange ein Geheimnis bleiben.
Da unser kleines Boot nur 3,5 N Wasser verdrängt, können wir ihm nur einen Ballast (B) von max. 1,5 N zumuten. ldeal wäre ein Ballastanteil von über 50%, aber das Rumpfgewicht des kleinen Schiffchens ist zu groß. Nun die Rechnung, ob es bei den vorgegebenen Annahmen ausreicht:
F x Hg = B x a
B = F x Hg / a
= 1,125 x 14,2 / 6 = 2,66 N
Also ist der Kiel entsprechend zu verlängern:
a = F x Hg / B
= 1,125 x 14,2/1,5
= 10,65 cm
Daraus folgt, dass der Ballastschwerpunkt Ca. 21 cm von der Wasserlinie entfernt sein sollte. Ob das wohl alles so richtig ist? Nur der praktische Versuch kann im Endeffekt zufrieden stellende Auskunft geben. Ich denke ohnehin, der praktische
Versuch zeigt sich günstiger als unsere Berechnungen, evtl. ist der Winddruck auch zu hoch angenommen.
Ferner ist zu berücksichtigen, dass Wind, Wellen und Wasser immer gleich bleiben. Für unser Modell im Maßstab von Ca. 1 :30 ist Windstärke 4 schon ein starker Sturm, und um bei diesem noch segeln zu können, brauchen wir eben den langen Kiel. 4 cm hohe Wellen ergeben im M 1 :30 auch 1,2 m Wellenhöhe für ein angenommenes Original. Das ist schon ganz ordentlich, und daraus folgt, dass ein kleines, vorbildgetreues Modell auch wirklich nur bei sehr schwachem Wind oder Flaute segeln kann.
Oft wird von Modellbauern bedauert, dass das Wasser, in dem unsere Modelle fahren, ja „leider" dasselbe bleibt wie das, in dem die Originale betrie ben werden, also nicht maßstäblich „verkleinerbar" ist. Meines Erachtens ist dies vollkommen in Ordnung, denn in einem maßstäblich „dünneren" Wasser, sprich einer Flüssigkeit mit geringerer Dichte würden unsere Modelle ja auch weniger Auftrieb haben, könnten u.U. also gar nicht schwimmen.
Nun, meine Boote sind jedenfalls je nach Typ alle mehr oder weniger gut geschwommen oder auch gesegelt. Ohne Hilfsantrieb sind sie fast immer zum Startpunkt zurückgekommen, wenn nicht, lag's meistens an der Fernsteueranlage. Die Berechnungen mögen im ersten Moment etwas kompliziert erscheinen, besonders wenn man nicht in der Materie „drin" ist. Mit einem normalen Taschenrechner kann man aber für ein einfaches Boot alles in etwa einer viertel Stunde erledigen.
![]() Original erschienen in der Zeitschrift Schiffsmodell des Neckar-Verlags 8/2001 Autor:Willi Hoppe. Sollten hiermit irgendwelche Rechte verletzt werden bitte melden. Ich werde dann den Artikel sofort entfernen.
Original erschienen in der Zeitschrift Schiffsmodell des Neckar-Verlags 8/2001 Autor:Willi Hoppe. Sollten hiermit irgendwelche Rechte verletzt werden bitte melden. Ich werde dann den Artikel sofort entfernen.



